Question

Find all the roots of y = x4 + 7x3 + 25x2 - 11x – 150

Answer 1

Given the equation :

`y=x^4+7x^3+25x^2-11x-150`

to find the roots of he function , y = 0

so,

`x^4+7x^3+25x^2-11x-150=0`

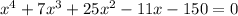
the factors of 150 are;

1 x 150 , 2 x 75 , 3 x 50 , 5 x 30 ,

We will check which number give y = 0

so, when x = 1 , y = -128

When x = -1 , y = -120

when x = 2 , y = 0

So, x = 2 is one of the roots

so ( x - 2 ) is one of the factors of the given equation :

Make a long division to find the other roots:

so,

`(x^4+7x^3+25x^2-11x-150)/(x-2)=x^3+9x^2+43x+75`

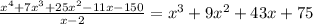
See the following image:

Now , we will repeat the steps for the result

the factors of 75

1 x 75 , 3 x 25 , 5 x 5

We will check which number give y = 0

when x = 1 , y = 128

when x = -1 , y = 40

When x = 3 , y = 312

when x = -3 , y = 0

so, x = -3 is another root

So, ( x + 3 ) is one of the factors

so, make a long division again to find the other roots:

`(x^3+9x^2+43x+75)/(x+3)=x^2+6x+25`

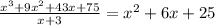
See the following image :

Now the last function :

`x^2+6x+25=0`

a = 1 , b = 6 , c = 25

`D=\sqrt[]{b^2-4\cdot a\cdot c}=\sqrt[]{36-4\cdot1\cdot25}=\sqrt[]{36-100}=\sqrt[]{-64}=i\sqrt[]{64}=\pm8i`

which mean the last equation has no real roots

So,

the roots of the given equation is just two roots

So, the answer is the roots of the given eaution is x = 2 and x = -3