The value of x equals the number of cubic units in a box that is 4 units high, 4 units deep, and 4 units wide.
Recall that the volume of a cube is given by
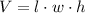
Where l is the length, w is the width, and h is the height of the cube.
We are given that all three sides are 4 units.
So, the volume is

x must be equal to this volume
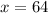
Take cube root on both sides of the equation
![\begin{gathered} \sqrt[3]{x}=\sqrt[3]{64} \\ \sqrt[3]{x}=\sqrt[3]{4^3} \\ \sqrt[3]{x}=4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/1pyghsieccy3gdmhh3bbai5yax31jdz4mu.png)
Therefore, the correct equation is the last option.
![\sqrt[3]{x}=4](https://img.qammunity.org/2023/formulas/mathematics/high-school/oo3fnieo9fooerc9w1l5fvnkswq5u5f1wk.png)