Question

3m^2-13m+20=0 what is the discriminant? use the discriminant to determine the number and type of solutions of the given equation ,3m^2-13m+20=0 is this equation one rational number, two irrational numbers, two nonreal complex numbers ,two rational numbers? The given equation ,3m^2- 13m+20=0, can be solved using the quadratic formula or zero-favtor property?

Answer 1

Answer:

The discriminant is -71

The discriminant is less than zero, the equation has no real roots

Step-by-step explanation:

Given the equation:

`3m^2-13m+20=0`

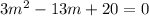
The discriminant is given as:

`D=b^2-4ac`

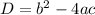
where a = 3, b = -13, c = 20

`\begin{gathered} D=(-13)^2-4(3)(20) \\ \\ =169-240 \\ =-71 \end{gathered}`

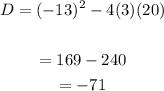
The discriminant is less than zero, the equation has no real roots