Question

Use a calculator to find θ to the nearest tenth of a degree, if 0° < θ < 360° and sin θ = -0.9945

Answer 1

Given:

`\sin \theta=-0.9945`

Using the inverse trigonometric function,

`\begin{gathered} \theta=\sin ^(-1)(-0.9945) \\ \theta=-83.988 \\ \theta\approx-84.0^0\text{ to the nearest tenth} \end{gathered}`

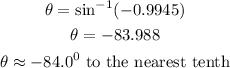
However, since the sine of the angle is negative, it shows that the angle is in the third or fourth quadrant.

Hence, the possible values of the angle are,

`\begin{gathered} \theta=-84+360=276.0^0 \\ \theta=180-(-84)=264.0^0 \end{gathered}`

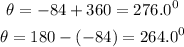
Therefore, the value of the angle to the nearest tenth of a degree is 264.0 degrees or 276.0 degrees.