Question

Would appreciate your help with this algebra question. Thank you!

Answer 1

`f(x)=-2x+4`

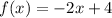
The above function is to be used if the value of x is between 0 and 8. On the other hand, the function to be used when x ≥ 8 is -5x + 11.

Since the interval to be checked is from 2 to 7, we will be using the first function which is -2x + 4.

To determine the rate of change between those intervals, we have the formula below:

`\text{rate of change = }(f(x_2)-f(x_1))/(x_2-x_1)`

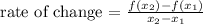
Let's solve f(x₂) first. Our x₂ = 7. Let's substitute the function above with x = 7.

`\begin{gathered} f(x)=-2x+4 \\ f(7)=-2(7)+4 \\ f(7)=-14+4 \\ f(7)=-10 \end{gathered}`

Let's solve f(x₁) first. Our x₁ = 2. Let's substitute the function above with x = 2.

`\begin{gathered} f(x)=-2x+4 \\ f(2)=-2(2)+4 \\ f(2)=-4+4 \\ f(2)=0 \end{gathered}`

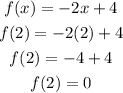
So, we now have the value of f(x₂) = -10, and f(x₁) = 0. Let's use these values to the formula of the rate of change above.

`\begin{gathered} \text{rate of change}=\frac{f(x_2)-f(x_1)^{}}{x_2-x_1} \\ \text{rate of change}=(-10-0)/(7-2) \\ \text{rate of change}=(-10)/(5) \\ \text{rate of change}=-2 \end{gathered}`

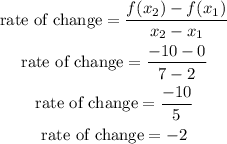
Since the rate of change is a negative number, the function is decreasing over the interval [2, 7].