1 Answer

Squirrelsama · Answer 1 · 2023-07-13T07:47:00+0000

We have the next given function:

$f(x)=\sqrt[3]{x}-2$

To find the first point, we need to use:

$\sqrt[3]{x}=0$

Solve the equation for x:

$(\sqrt[3]{x})^3=(0)^3$
x=0

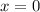
So, when x=0, we got the first point (0, -2), because:

$y=\sqrt[3]{x}-2$
y=0-2

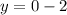
Then

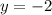
Let's find the points on right, let use x=8 and x=27

Replace on the function, when x=8

$y=\sqrt[3]{x}-2$
$y=\sqrt[3]{8}-2$
y=2-2

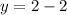
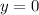
So, it represents the point (8,0)

Now, when x=27

$y=\sqrt[2]{27}-2$
y=3-2

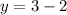
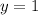
This corresponds to the point (27,1)

Now, for points on the left side:

When x=-8

$y=\sqrt[3]{-8}-2$
y=-2-2=-4

Which represents the point (-8,-4)

When x=-27

$y=\sqrt[3]{-27}-2$
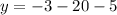
y=-3-20-5

Which represents the point (-27, -5)

Finally, graph these four points on the cartesian plane.

Please log in or register to add a comment.