Given:
The force is
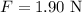
The area of the eardrum is
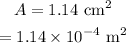
To find:
The maximum tolerable gauge pressure inside the eardrum
a) the pressure in mm of Hg
b) At what depth in freshwater would this person's eardrum rupture
Step-by-step explanation:
The pressure at the eardrum is
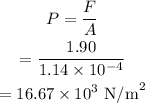
Hence, the pressure is
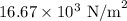
a)
We know,
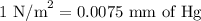
So,
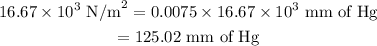
Hence, the pressure is 125.02 mm of Hg.
b)
The depth of fresh water is,
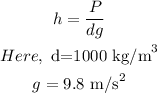
So,
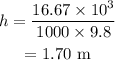
Hence, the depth of water is 1.70 m.