Question

What are all the ordered pairs that are solutions to the inequality 2x-3y>=12

Answer 1

To answer this question, we need to solve this inequality for y as follows:

`2x-3y\ge12`

Then, we have:

`-3y\ge12-2x\Rightarrow(-3y)/(-3)\leq(12)/(-3)-(2x)/(-3)\Rightarrow y\leq-4+(2x)/(3)`

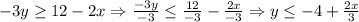
As we can see the direction of the inequality changed because we multiplied it by a negative number.

Then, if we can see the inequality, we find that the values that make this inequality true

are infinite values (the values of y are in function of the values of x).

Then, since we have the values given in the options, we need to check which of these values make the inequality true or we can graph a line for this inequality.

We have that the line is given by:

y = 2x/3 - 4

The x-intercept for this line is: