Question

Graph the line.y-1= 1/5 (x+4)

Answer 1

We are given the following equation:

`y-1=(1)/(5)(x+4​)`

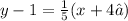
Using the distributive property:

`y-1=(1)/(5)x+(4)/(5)`

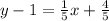
Adding 1 to both sides

`y=(1)/(5)x+(4)/(5)+1`

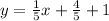
Solving the operations:

`y=(1)/(5)x+(9)/(5)`

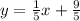
To graph this line we need two points through which the line passes. The first point can be obtained by making x = 0:

`\begin{gathered} y=(1)/(5)(0)+(9)/(5) \\ y=(9)/(5) \end{gathered}`

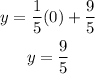
Therefore, the first point is (0,9/5).

The second point can be obtained by making x = 1, we get:

`\begin{gathered} y=(1)/(5)(1)+(9)/(5) \\ y=(10)/(5)=2 \end{gathered}`

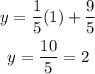
Therefore, the point is (1,2). Now we plot both points and join them with a line. The graph is: