Question

How do you find a vertex in intercept form

Answer 1

Quadratic functions can be written in vertex form, or

`y=a\mleft(x-h\mright)^2+k`

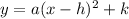
This is especially useful because the vertex of the function is found at the point (h, k).

We can find this form by completing squares, for instance, let y be:

`y=x^2+bx+c`

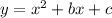
we can see that this equation is equal to

`y=x^2+2((b)/(2))x+((b)/(2))^2-((b)/(2))^2+c`

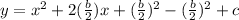
because

`2((b)/(2))=b`

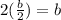
and

`((b)/(2))^2-((b)/(2))^2=0`

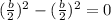
However, in this form, we can see that the first 3 terms are a perfect square, that is

`x^2+2((b)/(2))x+((b)/(2))^2=(x+(b)/(2))^2`

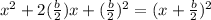
hence,

`\begin{gathered} y=x^2+bx+c \\ y=(x+(b)/(2))^2-((b)/(2))^2+c \end{gathered}`

If we define

`\begin{gathered} -((b)/(2))^2+c=k \\ \text{and} \\ h=(b)/(2) \end{gathered}`

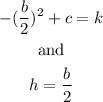
we have that

`y=(x+h)^2+k`

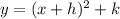
the constant a arise when you have a leading term different from 1 in x^2.