Question

Determine whether triangle DEF with vertices D(6, -6), E(39, -12), and F(24, 18) isscalene (no congruent sides), isosceles (two congruent sides), or equilateral (threecongruent sides).

Answer 1

We have three given points. We need to graph them, and then find the distances between them.

We need to remember that we can classify the triangles according to their sides:

1. A triangle with three congruent sides is an equilateral triangle.

2. A triangle with two congruent sides is an isosceles triangle.

3. A triangle with no congruent sides is a scalene triangle.

Additionally, we know that a segment is congruent to other when it has the same size as the other.

Then we can graph the three points as follows:

Now, we need to find the distances between the sides of the triangle using the distance formula as follows:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

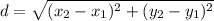
This is the distance formula for points (x1, y1) and (x2, y2).

Finding the distance between points D and E

The coordinates for the two points are D(6, -6) and E(39,-12), and we can label them as follows:

• (x1, y1) = (6, -6) and (x2, y2) = (39, -12)

Then we have:

`\begin{gathered} d=√((x_2-x_1)^2+(y_2-y_1)^2) \\ \\ d=√((39-6)^2+(-12-(-6))^2) \\ \\ d=√((33)^2+(-12+6)^2) \\ \\ d=√(33^2+(-6)^2)=√(1089+36)=√(1125) \\ \\ d_(DE)=√(1125)\approx33.5410196625 \end{gathered}`

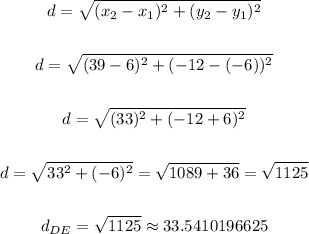
Therefore, the distance between points D and E is √1125.

And we need to repeat the same steps to find the other distances.

Finding the distance between points E and F

We can proceed similarly as before:

The coordinates of the points are E(39, -12) and F(24, 18)

• (x1, y1) = (39, -12)

,

• (x2, y2) = (24, 18)

Then we have:

`\begin{gathered} d=√((x_2-x_1)^2+(y_2-y_1)^2) \\ \\ d=√((24-39)^2+(18-(-12))^2) \\ \\ d=√((-15)^2+(18+12)^2)=√((-15)^2+(30)^2)=√(225+900) \\ \\ d_(EF)=√(1125)\approx33.5410196625 \end{gathered}`

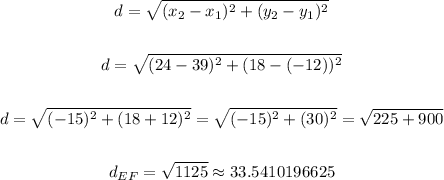
Then the distance between points E and F is √1125.

Finding the distance between F and D

The coordinates of the points are F(24, 18) and D(6, -6)

• (x1, y1) = (24, 18) and (x2, y2) = (6, -6)

Then we have:

`\begin{gathered} d=√((x_2-x_1)^2+(y_2-y_1)^2) \\ \\ d=√((6-24)^2+(-6-18)^2)=√((-18)^2+(-24)^2)=√(324+576) \\ \\ d=√(900)=30 \\ \\ d_(FD)=30 \end{gathered}`

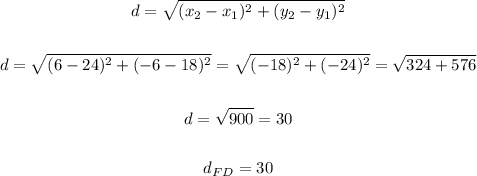
Now, we have the following measures for each of the sides of the triangle:

`\begin{gathered} \begin{equation*} d_(DE)=√(1125)\approx33.5410196625 \end{equation*} \\ \\ d_(EF)=√(1125)\approx33.5410196625 \\ \\ d_(FD)=30 \end{gathered}`

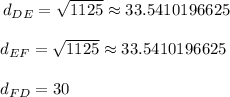
Therefore, in summary, according to the results, we have two sides that are congruent (they have the same size). Therefore, the triangle DEF is an isosceles triangle.