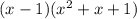Given that the sum of two cubes can be factored by using the formula
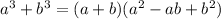
a) To verify the formula by multiplying the right side equation
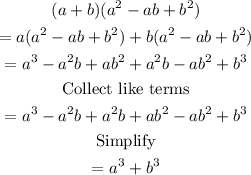
Hence,
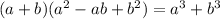
b) To factor
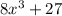
Using the sum of two cubes formula, i.e
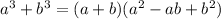
Factorizing the expression gives
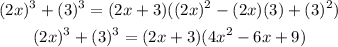
Hence, the answer is
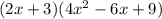
c) Given that one of the factors of a³ - b³ is a- b, the quadratic factor of a³ - b³ can be deduced by applying the differences of cubes formula below
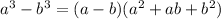
Expanding the right side equations
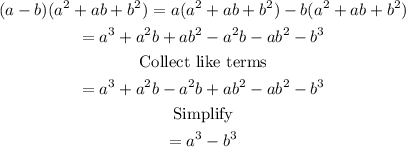
Hence, the quadratic factor is
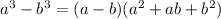
d) To factor the expression
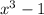
By applying the differences of cubes formula
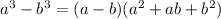
Factorizing the expression gives
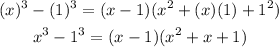
Hence, the answer is