Question

Josie sold 965 tickets to a local car show for a total of $4,335.00. A ticket for childrencosts $3.00 and an adult ticket costs $5.00. How many of each ticket did she sell?

Answer 1

`\begin{gathered} 245\text{ children tickets were sold.} \\ \text{ 720 adult tickets were sold.} \end{gathered}`

Explanation:

To approach this situation, we need to create a system of linear equations.

Let x be the number of children

Let y be the number of adults

For equation 1)

Since the sum of the tickets sold are 965, it means children plus adults is 965

`x+y=965`

For equation 2)

Since the price for children is $3, the adult ticket costs $5, and the total of tickets sold is $4,335:

`3x+5y=4335`

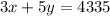
Now, we can solve this by using the substitution method, isolating one of the variables in equation 1 and plugging it into equation 2.

`y=965-x`

Plug it into equation 2:

`3x+5(965-x)=4335`

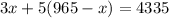
Solve for x.

`\begin{gathered} 3x+4825-5x=4335 \\ 5x-3x=4825-4335 \\ 2x=490 \\ x=(490)/(2) \\ x=245 \\ 245\text{ children tickets were sold.} \end{gathered}`

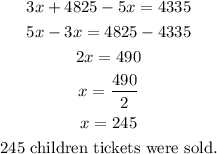
Knowing the value for x, we can plug it into equation 1, and solve for y.

`\begin{gathered} y=965-245 \\ y=720\text{ } \\ \text{ 720 adult tickets were sold.} \end{gathered}`