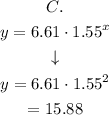1 Answer

Davuz · Answer 1 · 2023-10-13T10:48:32+0000

Exponential regression

In order to find the exponential regression we are going to select some values of the given data.

STEP 1

An special value is when x=0.

On the table we can see that when x=0 then y=9

Replacing x by 0 in the given choices, we have that:

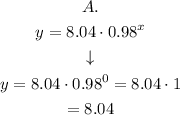
$\begin{gathered} A\text{.} \\ y=8.04\cdot0.98^x \\ \downarrow \\ y=8.04\cdot0.98^0=8.04\cdot1 \\ =8.04 \end{gathered}$

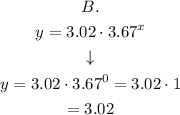
$\begin{gathered} B\text{.} \\ y=3.02\cdot3.67^x \\ \downarrow \\ y=3.02\cdot3.67^0=3.02\cdot1 \\ =3.02 \end{gathered}$

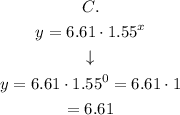
$\begin{gathered} C\text{.} \\ y=6.61\cdot1.55^x \\ \downarrow \\ y=6.61\cdot1.55^0=6.61\cdot1 \\ =6.61 \end{gathered}$

$\begin{gathered} D\text{.} \\ y=2.27\cdot2.09^x \\ \downarrow \\ y=2.27\cdot2.09^0=2.27\cdot1 \\ =2.27 \end{gathered}$

Observing the results we have that the two choices with closer results to 9 are A (with 8.04) and C (with 6.61)

Now, we are going to select two additional values from the table in order to find which is the best answer: A or C.

Let's take x=1.

When x = 1, then y=10.

Replacing on the equation A we have:

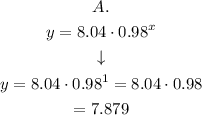
$\begin{gathered} A\text{.} \\ y=8.04\cdot0.98^x \\ \downarrow \\ y=8.04\cdot0.98^1=8.04\cdot0.98 \\ =7.879 \end{gathered}$

and for the equation C:

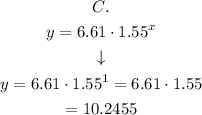
$\begin{gathered} C\text{.} \\ y=6.61\cdot1.55^x \\ \downarrow \\ y=6.61\cdot1.55^1=6.61\cdot1.55 \\ =10.2455 \end{gathered}$

For x=1, the nearest result is from the equation C.

Let's verify what happens when x=2.

When x=2 then y=16. Replacing on the equation A we have:

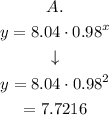
$\begin{gathered} A\text{.} \\ y=8.04\cdot0.98^x \\ \downarrow \\ y=8.04\cdot0.98^2 \\ =7.7216 \end{gathered}$

and for the equation C:

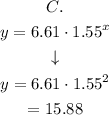
$\begin{gathered} C\text{.} \\ y=6.61\cdot1.55^x \\ \downarrow \\ y=6.61\cdot1.55^2 \\ =15.88 \end{gathered}$

Again, for x=2, the nearest result is from the equation C.

Then, we can conclude that the best candidate is equation C.

We could try other values of x to double check:

$\begin{gathered} C\text{.} \\ y=6.61\cdot1.55^x \\ \downarrow \\ y=6.61\cdot1.55^2 \\ =15.88 \end{gathered}$