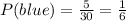Question

Please help me with this quickly, the questions says to show work or explain but I want explanation, thank you!

Answer 1

- Experimental probability is the probability gotten from conducting experiments and it is different from theoretical probability which is derived from hypothetical situations.

- In this question, the hypothetical situation that leads to the theoretical probabilities of getting a red, an orange, and so on, is the fact that the question already said the smallest section of the circle is 1/16 and every other portion is a multiple of this.

- The experimental probabilities are gotten from the table and the formula for calculating this probability is given below:

`\begin{gathered} Given\text{ Event \lparen E\rparen,} \\ P(E)=\frac{Number\text{ of times an event occurs}}{Total\text{ number of trials}} \end{gathered}`

- Thus, we can proceed to find the experimental probabilities of finding any of these colors as follows:

Orange:

`\begin{gathered} E=\text{ Event of spinning an Orange} \\ P(orange)=(3)/(30)=(1)/(10) \end{gathered}`

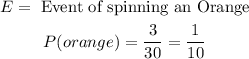
Green:

`P(green)=(6)/(30)=(1)/(5)`

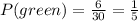
Blue:

`P(blue)=(5)/(30)=(1)/(6)`