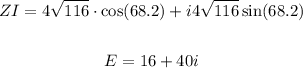Question

Complex numbers are used to describe current. I voltage, E, and impedance, Z. These three quantities are related by the equation E = IZ. Given two ofthese quantities, solve the equation E = IZ for the missing variable.I = 4 + 4i, Z= 7+3iE=(Simplify your answer. Type your answer in the form a+b/. Use integers or fractions for any numbers in the expression.)

Answer 1

We have the following equation to solve

`E=I\cdot Z`

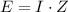
Where E, I, and Z are complex numbers, therefore let's put it in numbers

`E=(4+4i)(7+3i)`

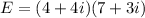
We can solve it directly into the rectangular form by doing the distrutive

Then

`(4+4i)(7+3i)=28+12i+28i+12i^2`

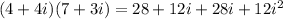
Remember that

`i^2=-1`

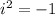
Then

`\begin{gathered} (4+4\imaginaryI)(7+3\imaginaryI)=28+12i+28i-12 \\ \\ (4+4\imaginaryI)(7+3\imaginaryI)=16+40i \end{gathered}`

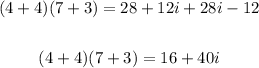
Now we have completely solved the problem!

`E=16+40i`

______________________

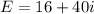
The second solution (usual)

When we have real engineering problems, we like to do multiplication and division with the polar form, then let's convert Z and I to the polar form

`\begin{gathered} I=4+4i=4√(2)\angle45° \\ \\ Z=7+3i=√(58)\angle23.2° \end{gathered}`

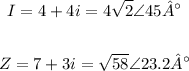
Now to do the multiplication we multiple the magnitude and sum the phases (angles)

We already have the result, now just put it in the rectangular form

`\begin{gathered} ZI=4√(116)\cdot\cos(68.2)+i4√(116)\sin(68.2) \\ \\ E=16+40i \end{gathered}`