Question

If each side of an equilateral triangle is 2 inches long, then what is the area of the triangle?

Answer 1

The image below represents the equilateral triangle of 2 inches long

From the triangle above, the given values include

`\begin{gathered} a=2in \\ b=2in \\ c=2in \end{gathered}`

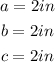
Concept:

To calculate the area of the triangle, we will use Heron's formula below

`\begin{gathered} A=\sqrt[]{s(s-a)(s-b)(s-c)} \\ \text{where,s = semi perimter} \\ s=(a+b+c)/(2) \end{gathered}`

Step 1:

Calculate the semi perimeter s

`\begin{gathered} s=(a+b+c)/(2) \\ s=(2in+2in+2in)/(2) \\ s=(6in)/(2) \\ s=3in \end{gathered}`

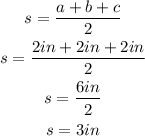
Step 2:

Substitute the value of s,a,b,c in the heron's formula

`\begin{gathered} A=\sqrt[]{s(s-a)(s-b)(s-c)} \\ A=\sqrt[]{3(3-2)(3-2)(3-2)} \\ A=\sqrt[]{3*1*1*1} \\ A=\sqrt[]{3} \\ A=1.73in^2 \end{gathered}`

Hence,

The area of the triangle = 1.73 squared inches