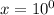Step-by-step explanation:
Part A:
The image is given below as
Concept:
Using the linear pairs theorem, we will have that
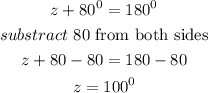
Also from the image of the question, we can deduce that
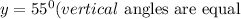
Hence,
To calculate the value of x, we will use the sum of angles in a triangle
The sum of angles in a triangle gives
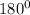
By substtituting the values, we will have
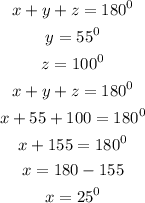
Hence,
The final answer for x in part A is
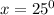
Part B:
From the image in the question we can see that angle segmen makes up a right angle
Hence,
We will have the relation below
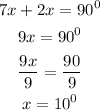
Hence,
The final answer for x in part B is