A trinomial square has two possible forms:
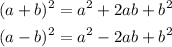
So, for us to check if
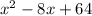
Is a trinomial square, we first check if the first and thrid terms are positive, because both options has positive first and thrid terms, even if a or b are negative, because they are squared in the process.
Both are positive, x² and 64.
Now, by comparison, we see that, in thi case we would have:
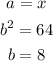
If it is a trinomial square, than the middle term has to be:
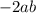
We use the negative form because we have a negative middle term.
So, let's see if it checks out:
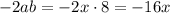
We got -16x, but the middle term is -8x, they don't match.
Since they don't match, the given expression is not a trinomial square. The answer is No.