Question

A ship's wheel has a moment of inertia of 0.930 kilogram·meters squared. The inner radius of the ring is 26 centimeters, and the outer radius of the ring is 32 centimeters. Disagreeing over which way to go, the captain and the helmsman try to turn the wheel in opposite directions. The captain applies a force of 314 newtons at the inner radius, while the helmsman applies a force of 290 newtons at the outer radius. What is the magnitude of the angular acceleration of the wheel?

Answer 1

We can use the formula of the moment of inertia given by:

`r\cdot F=I\alpha`

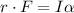
Where:

r = Distance from the point about which the torque is being measured to the point where the force is applied

F = Force

I = Moment of inertia

α = Angular acceleration

So:

`\begin{gathered} r\cdot F=(-0.26*314+290*0.32)=92.8-81.64=11.16 \\ I=0.930 \\ so,_{\text{ }}solve_{\text{ }}for_{\text{ }}\alpha: \\ \alpha=(r\cdot F)/(I) \\ \alpha=(11.16)/(0.930) \\ \alpha=(12rad)/(s^2) \end{gathered}`

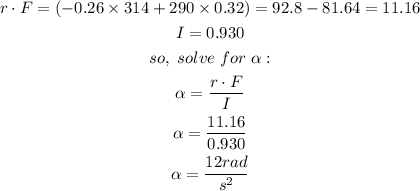
Answer:

12 rad/s²