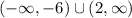To answer this question, we need to have into account the following:
1. In the context of interval notation, the word "or" can be represented by the symbol "U".
2. We need to rearrange the inequality -x > 6 in a way that we have positive x.
We can proceed as follows:
Case x>2
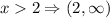
We can express the inequality in this way because it expresses all of the values greater than 2, and these values tend to the positive infinity. We have parenthesis here since the values are not equal to 2 (only greater than 2).
Case -x > 6
If we multiply both sides of the inequality by -1, we need to reverse the direction of the inequality as follows:
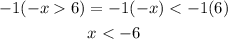
Now, we have all of the values less than -6, not equal, and because of this, we have to use parenthesis:
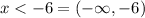
Therefore, we can say that:
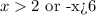
Can be expressed in interval notation as:
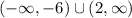
In summary, the answer to this question is: