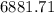First, divide the annual interest rate by 2 to find the semiannual interest rate:
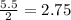
Next, identify the number of periods when the 2.75% increase will be appliad. In a period of 10 years, there are 20 semiannual periods.
Each period, the initial investment gets multiplied by a factor of:
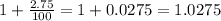
Over 20 semiannual periods, the initial investment will get multiplied by a factor of:
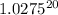
Therefore, after 10 years, the amount of money in the account is:
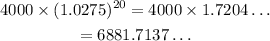
To the nearest cent, the amount of money in the account will be: