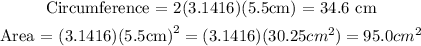Question

Find the circumference and area of each. Round for the nearest tenth:

1) a circle has a radius of 2 meters
2) a circle has a diameter of 16 cm
3) a circle has a radius of 8ft
4) a circle has a diameter of 11 cm

Answer 1

Answers:

1) C = 12.6 m

A = 12.6 m²

2) C= 50.3 cm

A = 201.1 cm²

3) C= 50.3 ft

A = 201.1 ft²

4) C= 34.6 cm

A = 95.0 cm²

Step-by-step explanation:

The circumference and area of a circle with radius r can be calculated as:

`\begin{gathered} \text{Circumference = 2}\pi r \\ Area\text{ = }\pi r^2 \end{gathered}`

Where π is approximately 3.1416

Then, for each option, we get:

1) Replacing the radius by 2 m, we get:

`\begin{gathered} \text{Circumference}=2(3.1416)(2m)=12.6m \\ \text{Area}=(3.1416)(2m)^2=(3.1416)(4m^2)=12.6m^2 \end{gathered}`

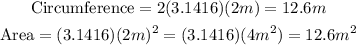
2) If the diameter is 16 cm, the radius is 8 cm because the radius is half the diameter. So, replacing r by 8 cm, we get:

`\begin{gathered} \text{Circumference = 2(3.1416)(8cm) = 50.3cm} \\ \text{Area = (3.1416)(8cm)}^2=(3.1416)(64cm^2)=201.1cm^2 \end{gathered}`

3) Replacing r by 8 ft, we get:

`\begin{gathered} \text{Circumference = 2(3.1416)(8ft) = 50.3ft} \\ \text{Area = (3.1416)(8ft)}^2=(3.1416)(64ft^2)=201.1ft^2 \end{gathered}`

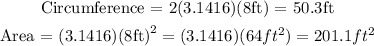
4) If the diameter is 11 cm, the radius is 11/2 = 5.5 cm, so:

`\begin{gathered} \text{Circumference = 2(3.1416)(5.5cm) = 34.6 cm} \\ \text{Area = (3.1416)(5.5cm)}^2=(3.1416)(30.25cm^2)=95.0cm^2 \end{gathered}`