Question

`( - 4x + 2y \leqslant 4 )(x + 4y \ \textgreater \ - 10)`how do I graph this

Answer 1

Given the system of inequalities

`\begin{gathered} -4x+2y\leq4 \\ x+4y>-10 \end{gathered}`

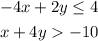
We start by getting the plot of one of these inequalities. Let's start on -4x + 2y ≤ 4. This equation can be rewritten as

`\begin{gathered} 2y\leq4+4x \\ y\leq2+2x \end{gathered}`

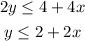
Initially, we consider the equation

`y=2+2x`

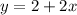
Plotting the equation, we have

Considering the values of these function at

`y\leq2+2x`

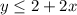
Let's use the same steps implemented above for the second inequality. We have

`\begin{gathered} 4y>-10+x \\ y>(x-10)/(4) \end{gathered}`

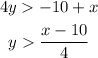
Plotting this we have,

The dashed line represents the values that are not included in the equation, as a present for inequalities with less than or greater than. The shaded region represents the solution

After plotting the two inequalities individually, we now superimpose the two graphs. We get

where the darker region represents the solution of the inequalities.