Question

The area of a triangle is 15. Two of the side lengths are 5.5 and 7.5 and the includedangle is acute. Find the measure of the included angle, to the nearest tenth of adegree.

Answer 1

α =46º

1) Let's start by gathering the data:

S = 15 u²

a= 5.5

b= 7.5

Sketcing out:

2) One of the formulas to find out the area of a triangle is:

`S=(ab\cdot\sin (\alpha))/(2)`

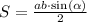
Plugging the given data into the formula we have:

`\begin{gathered} 15=(5.5\cdot7.5\sin (\alpha))/(2)\text{ }*2 \\ 30\text{ =41.25}\cdot\sin (\alpha) \\ (30)/(41.25)=\frac{\text{41.25}\cdot\sin (\alpha)}{41.25} \\ 0.72=\sin (\alpha) \end{gathered}`

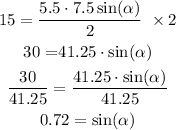
2.2) Since we want to know the measure of that angle, then let's make use of the arcsine of (0.72)

`\begin{gathered} \alpha=\sin ^(-1)(0.72) \\ \alpha=46.05\approx46 \end{gathered}`

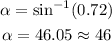
3) Hence, the missing acute angle is α =46º (rounded off to nearest whole number)