Part A.
The quadratic equation,

is equivalent to
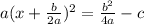
In our case a=1, b=-3 and c=-18. Then, by substituting these value into the last result, we have
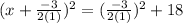
which gives
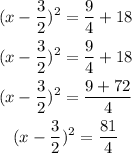
Therefore, the answer for part A is:
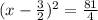
Part B.
Now, we need to solve the last result for x. Then, by applying square root to both sides, we have
![x-(3)/(2)=\pm\sqrt[]{(81)/(4)}](https://img.qammunity.org/2023/formulas/mathematics/college/xd9ld2f1lyvycxbwqsgvjtnffuv6as9vz4.png)
which gives
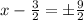
then, by adding 3/2 to both sides, we obtain
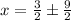
Then, we have 2 solutions,
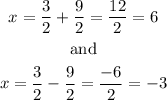
Therefore, the answer for part B is: -3, 6