Question

A Gallup survey of 2322 adults (at least 18 years old) in the U.S. found that 408 of them have donated blood in the past two years. Construct a 90% confidence interval for the population proportion of adults in the U.S. who have donated blood in the past two years. Round your answer to three decimal places.

Answer 1

Answer: aA 90% confidence interval for the population proportion of adults in the U.S. who have donated blood in the past two years = (0.163,0.189)

Explanation:

Let p = population proportion of adults in the U.S. who have donated blood in the past two years.

Given: A Gallup survey of 2322 adults (at least 18 years old) in the U.S. found that 408 of them have donated blood in the past two years.

Sample size: n= 2322

Sample proportion
`q=(408)/(2322)=0.176`

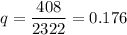
Critical z-value for 90% confidence level : z*=1.645

The confidence interval for population proportion:

`q\pm z^*(\sqrt{(q(1-q))/(n)})`

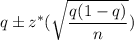
A 90% confidence interval for the population proportion of adults in the U.S. who have donated blood in the past two years:

`0.176\pm (1.645)(\sqrt{(0.176(1-0.176))/(2322)})\\\\=0.176\pm (1.645)(0.0079)\\\\=(0.176\pm0.013)\\\\=(0.176-0.013,0.176+0.013))\\\\=(0.163,0.189)`

Hence,