Answer: aA 90% confidence interval for the population proportion of adults in the U.S. who have donated blood in the past two years = (0.163,0.189)
Explanation:
Let p = population proportion of adults in the U.S. who have donated blood in the past two years.
Given: A Gallup survey of 2322 adults (at least 18 years old) in the U.S. found that 408 of them have donated blood in the past two years.
Sample size: n= 2322
Sample proportion
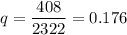
Critical z-value for 90% confidence level : z*=1.645
The confidence interval for population proportion:
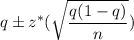
A 90% confidence interval for the population proportion of adults in the U.S. who have donated blood in the past two years:

Hence,