Given:
Data x: 24, 28, 26, 30, 32
n = 5
Asked: What is the standard deviation of the population?
Formula:
![\text{standard deviation = }\sqrt[]{\frac{\sum ^{}_{}(x-\bar{x})^2}{n}}](https://img.qammunity.org/2023/formulas/mathematics/college/sa36hnmwow9lj50ubyqg2tupmmfuxmqaq9.png)
Solution:
Step 1: We will get the average of the data given.
NOTE: Bar x is also the mean or the average.
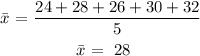
Step 2: We will subtract the mean from each number.
Step 3: We will square the differences and get the summation.
Step 4: We will substitute the acquired values to find the standard deviation using the formula above.
![\begin{gathered} \text{standard deviation = }\sqrt[]{\frac{\sum ^{}_{}(x-\bar{x})^2}{n}} \\ \text{standard deviation = }\sqrt[]{\frac{40^{}}{5}}\text{ } \\ \text{standard deviation = 2}\sqrt[]{2}\text{ = }2.828427125 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/pyh40gxp1wz06d70xcw7s2n33ufndfi3su.png)
ANSWER: standard deviation = 2.83 (Rounded off to 2 decimal places)