Solving for area of first figure
Recall the following formula for area of 2D figures
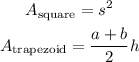
The first figure consist of 2 figures with a square of side length of 2.5 cm, and a trapezoid with length 2.5 cm for the upper base, 5 cm for the lower base, and 2 cm for the height.
Calculate the area by getting the sum of the areas of the two figures

The area of the first figure therefore is 13.75 square centimeters.
Solving for the area of the second figure
Recall the following areas for 2D figures
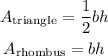
Using the same procedures as above, we get the following
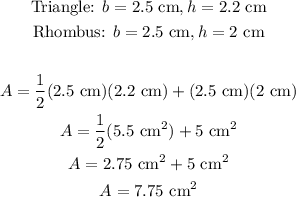
Therefore, the area of the second figure is 7.75 square centimeters.