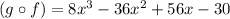Given two functions f(x) and g(x), its composition will be:
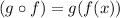
It is read g compound f or simply said to g we are going to fill it with f. So, you have
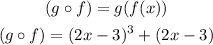
To expand the binomial, apply the binomial formula to the cube, that is:
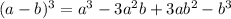
So, you have
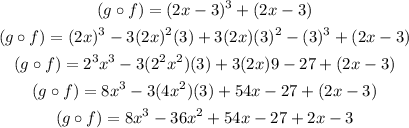
Finally, operate similar terms