Question

Prove that 1+3+5+......2n-1=n²

Answer 1

As given by the question

There are given that the series

`1+3+5+\cdots+(2n-1)=n^2`

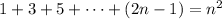
Now,

For step 1:

Put n=1

Then LHS =1

And

`\begin{gathered} R\mathrm{}H\mathrm{}S=(n)^2 \\ =(1)^2 \\ =1 \end{gathered}`

So,

`\therefore L.H.S=R.H.S`

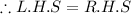
P(n) is true for n=1.

Now,

Step 2:

Assume that P(n) istrue for n=k

Then,

`1+3+5+\cdots+(2n-1)=k^2`

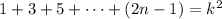
Adding 2k+1 on both sides

So, we get:

`1+3+5\ldots+(2k-1)+(2k+1)=k^2+(2k+1)=(k+1)^2`

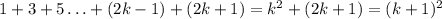
P(n) is true for n=k+1

By the principle of mathematical induction P(n) is true for all natural numbers n.

Hence,

`1+3+5+\cdots+(2n-1)=n^2`

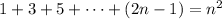
For all n.

Hence proved.