The law of sine states that the ratio of Sine A and side a is just equal to the ratio of Sine B and side b which is also equal to the ratio of Sine C and side c. In formula, we have:
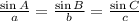
where the big letter A, B, C are the angles and the small letters are the side opposite of the angle.
In our triangle, we have angle 19 and its opposite side is "x" whereas the angle opposite of the side that has a length of 32 units is unknown.
To solve the unknown angle, we know that the total measure of the angle in a triangle is 180 degrees. Therefore, the measure of the missing angle is 180 - 19 - 26 = 135 degrees.
So, going back to the law of sine, we have:

Therefore, the measure of the side x is approximately 14.73 units.
To solve the length of the other side, say y, the side opposite angle 26, we can make use of the law of sine again.
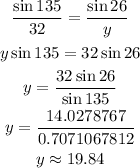
The length of the other missing side opposite angle 26 is approximately 19.84 units.