Given: The bearing and distance of a ship from Akron(A) through Bellville(B) to Compton(C)
To Determine: The distance travelled and the angles
Solution
The diagram of the journey can be represented as shown below
Let us solve for BC using cosine rule

The total distance travelled is
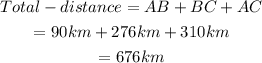
Using sine rule, we can determine the measure of angle C

Also know that the sum of angles in a triangle is 180 degree. Therefore
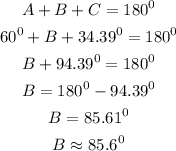
The bearing of Compton from Bellville(B) is
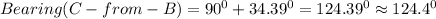
The bearring of Akron(A) from Compton(C) is

In summary
The total distance travelled is 676km
The bearing of Compton from Bellville is 124.4 degrees, and the bearing of Akron from Compton is 304.4 degrees