Question

How do you find the length of a side of a triangle when given the length of only one other side?

Answer 1

WE can find the sides if the triangle by apply the Sine rule :

`(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

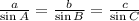
where, a,b & c are the sides of triangle

For eg :

Consider an triangle with one side AB = 5

and angles A = 60, angle B = 45 and angle C= 75

So, substitute the value in the expression of Sine

`\begin{gathered} (BC)/(\sin A)=(AC)/(\sin B)=(AB)/(\sin C) \\ (BC)/(\sin 60)=(AC)/(\sin 45)=(5)/(\sin 75) \\ \text{ Substitute the values :} \\ (BC)/(\sin60)=(AC)/(\sin45)=(5)/(\sin75) \\ (BC)/(0.866)=(AC)/(0.707)=(5)/(0.965) \\ \text{ Simplify : }(AC)/(0.707)=(5)/(0.965) \\ (AC)/(0.707)=(5)/(0.965) \\ AC=(5)/(0.965)*0.707 \\ AC=3.66 \\ \text{Now, Simplify: }(BC)/(0.866)=(5)/(0.965) \\ BC=(5)/(0.965)*0.866 \\ BC=4.4 \end{gathered}`

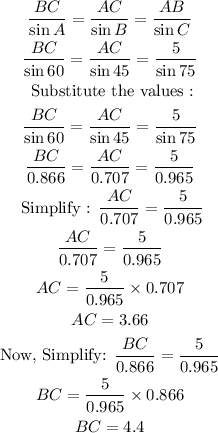
The sides : AB = 5, AC = 3.66 & BC = 4.4