Question

What is the value of x?12 units15 units20 units25 units

Answer 1

12 units

Step-by-step explanation

Step 1

set the equations:

we have three rectangles triangles,so

Let

triangle STR and triangle RTQ

so,

a) for triangle STR

let

`\begin{gathered} \text{ hypotenuse: RS} \\ \text{adjacent side;RT}=x \\ \text{opposite side:ST=9} \\ \text{angle:m}\angle R \end{gathered}`

so, we can use the Pythagorean theorem,it states that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse (the side opposite the right angle)

so

`\begin{gathered} (RS)^2=(ST)^2+(RT)^2 \\ (RS)^2=(9)^2+(x)^2\rightarrow equation(1) \end{gathered}`

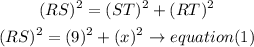
b) for triangle RTQ

`\begin{gathered} \text{ hypotenuse: RQ} \\ \text{adjacent side;TQ}=16 \\ \text{opposite side:RT=x} \\ \text{angle:m}\angle Q \end{gathered}`

again, let's use the P.T.

`\begin{gathered} (RQ)^2=(RT)^2+(TQ)^2 \\ (RQ)^2=(x)^2+(16)^2\Rightarrow\text{equation}(2) \end{gathered}`

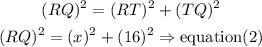
c)

we know the triangles STR and SQR are similar, so

`m\angle R=m\angle Q`

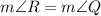
also,

`\begin{gathered} \tan m\angle R=\tan m\angle Q \\ \frac{oppositeside_R}{\text{adjacent sideR}}=\frac{oppositeside_Q}{\text{adjacent sideQ}} \\ (9)/(x)=(SR)/(RQ)\rightarrow equation\text{ (3)} \end{gathered}`

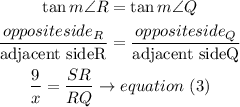
finally, we can set a new equation with triangle SQR

d)again, let's use the P.T.

`\begin{gathered} (SQ)^2=(SR)^2+(RQ)^2 \\ \text{replace} \\ (9+16)^2=(SR)^2+(RQ)^2 \\ (25)^2=(SR)^2+(RQ)^2\rightarrow equation(4) \end{gathered}`

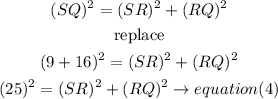
Step 2

solve the equations

`\begin{gathered} (RS)^2=(9)^2+(x)^2\rightarrow equation(1) \\ (RQ)^2=(x)^2+(16)^2\Rightarrow\text{equation}(2) \\ (9)/(x)=(SR)/(RQ)\rightarrow equation\text{ (3)} \\ (25)^2=(SR)^2+(RQ)^2\rightarrow equation(4) \end{gathered}`

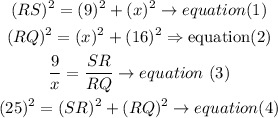
solution:

a)

`\begin{gathered} \text{isolate (x) in equation(1) and (2) and set equal } \\ (RS)^2=(9)^2+(x)^2\rightarrow equation(1) \\ (RS)^2-(9)^2=(x)^2 \\ \text{and} \\ (RQ)^2=(x)^2+(16)^2\Rightarrow\text{equation}(2) \\ (RQ)^2-\mleft(16\mright)^2=(x)^2 \\ (RQ)^2-(16)^2=(x)^2 \\ \text{hence} \\ (RS)^2-(9)^2=(RQ)^2-(16)^2 \\ \text{isolate (RS)}^2 \\ (RS)^2=(RQ)^2-(16)^2+(9^2) \\ (RS)^2=(RQ)^2-175\rightarrow equation(5) \end{gathered}`

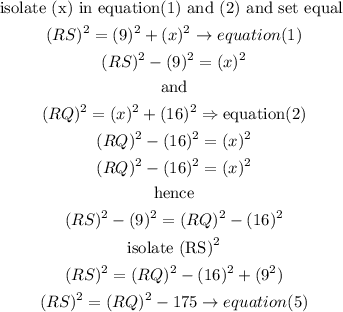
b) now using equation (4) and equation(5) we can set system of 2 equations and 2 unknown values, so

`\begin{gathered} (25)^2=(RS)^2+(RQ)^2\rightarrow equation(4) \\ (RS)^2=(RQ)^2-175\rightarrow equation(5) \\ replce\text{ eq(5) into equation (4)} \\ (25)^2=(RS)^2+(RQ)^2\rightarrow equation(4) \\ so \\ (25)^2=(RQ)^2-175+(RQ)^2 \\ 625+175=(RQ)^2+(RQ)^2 \\ 800=2(RQ)^2 \\ \mleft(RQ\mright)^2=(800)/(2) \\ (RQ)^2=400 \\ RQ=20 \end{gathered}`

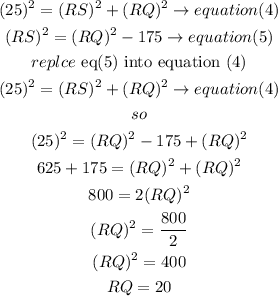
so

RQ=20

now, replace in equation (5) to find RS

`\begin{gathered} (RS)^2=(RQ)^2-175\rightarrow equation(5) \\ (RS)^2=(20)^2-175 \\ (RS)^2=225 \\ RS=\sqrt[]{225} \\ RS=15 \end{gathered}`

RS=15

finally, replace RS in equation (1) to find x

`\begin{gathered} (RS)^2=(9)^2+(x)^2\rightarrow equation(1) \\ (15)^2=(9)^2+(x)^2 \\ 225-81=x^2 \\ 144=x^2 \\ \sqrt[]{144}=\sqrt[]{x^2} \\ 12=x \end{gathered}`

therefore, the answer is

12 units

I hope this helps yuo