Question

Marks wants to paint a mural. He had 1 1/5 gallons of yellow paint, 1 1/6 gallons of green paint and 7/8 gallon of blue paint. Mark plan to use 3/4 gallons of each paint color. How many gallons of paint will he have left painting the mural?

Answer 1

Yello paint: 1 1/5

Green paint: 1 1/6

Blue paint: 7/8

After using 3/4 of each paint color, we have

- Yellow:

`\begin{gathered} 1+(1)/(5)-(3)/(4) \\ (5)/(5)+(1)/(5)-(3)/(4) \end{gathered}`

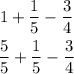
The least common multiple of 5 and 4 is 20, then...

`\begin{gathered} (5\cdot4)/(5\cdot4)+(1\cdot4)/(5\cdot4)-(3\cdot5)/(4\cdot5) \\ (20)/(20)+(4)/(20)-(15)/(20) \\ (20+4-15)/(20) \\ (9)/(20) \end{gathered}`

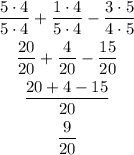
So, for yellow paint, we will have 9/20 gallons

- Green:

`\begin{gathered} 1+(1)/(6)-(3)/(4) \\ (6)/(6)+(1)/(6)-(3)/(4) \end{gathered}`

The LCM of 6 and 4 is 12

`\begin{gathered} (6\cdot2)/(6\cdot2)+(1\cdot2)/(6\cdot2)-(3\cdot3)/(4\cdot3) \\ (12)/(12)+(2)/(12)-(9)/(12) \\ (12+2-9)/(12) \\ (5)/(12) \end{gathered}`

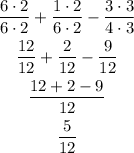
So, for green paint, we will have 5/12 gallons

- Blue:

`(7)/(8)-(3)/(4)`

LCM of 4 and 8 is 8

`\begin{gathered} (7)/(8)-(3\cdot2)/(4\cdot2) \\ (7)/(8)-(6)/(8) \\ (7-6)/(8) \\ (1)/(8) \end{gathered}`

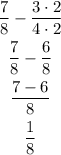
So, for blue paint, we will have 1/8 gallons

Now, we add them upp in order to obtain our anwser:

`(9)/(20)+(5)/(12)+(1)/(8)`

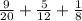
The LCM of 8, 12 and 20 is 120

`\begin{gathered} (9\cdot6)/(20\cdot6)+(5\cdot10)/(12\cdot10)+(1\cdot15)/(8\cdot15) \\ (54)/(120)+(50)/(120)+(15)/(120) \\ (54+50+15)/(120) \\ (119)/(120) \end{gathered}`

In conclusion, he will have left 119/120 gallons of paint