Question

There is a population of 405,000 bacteria in a colony. If the number of bacteria doubles every 44 hours, what will the population be 176 hours from now?

Answer 1

Since the population doubles every 44 hours, it can be modeled using an exponential equation as follows:

`P(t)=405,000*2^{(t)/(44)}`

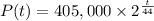
Where t is the time since the population was 405,000 measured in hours.

Replace t=176 to find the population after 176 hours:

`\begin{gathered} P(176)=405,000*2^{(176)/(44)} \\ =405,000*2^4 \\ =405,000*16 \\ =6,480,000 \end{gathered}`

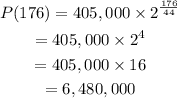
Therefore, the population after 176 hours will be 6,480,000