Question

Anthony has a total of $4.20 in nickels, dimes and quarters. If hehas 6 more dimes than nickels and three times as many quartersas nickels, how many of each kind of coin does he have?

Answer 1

We are given a problem that can be solved by a system of equations. Let N be the number of nickels, D the number of dimes, and Q the number of Quarters. Since in total he has 4.2, this means mathematically:

`N+D+Q=4.2,\text{ (1)}`

We are told that he has 6 more dimes than nickels, this can be written like this:

`D=6N,\text{ (2)}`

We are told that he has three-time Quarters than nickles, this is:

`Q=3N,\text{ (3)}`

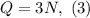
Now, if we replace equation (2) and (3) in equation (1), we get:

`N+6N+3N=4.2`

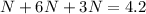
Solving for N, we get;

`\begin{gathered} 10N=4.2 \\ N=(4.2)/(10)=0.42 \end{gathered}`

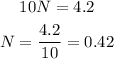
Replacing the value of N in equation (2), we get:

`\begin{gathered} D=6N \\ D=6(0.42)=2.52 \end{gathered}`

Now we replace the value of N in equation (3):

`\begin{gathered} Q=3N \\ Q=3(0.42)=1.26 \end{gathered}`

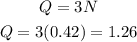
Therefore, he has, 0.42 in nickels, 2.52 in dimes, and 1.26 in quarters.