To answer this question, we need to substitute the value of x into the given "rule" for the function as follows:
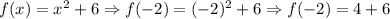
Therefore, we have:
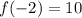
Therefore, the ordered pairs (x, f(x)) are (-2, 10).
We can graph this point on the graph as follows:
Then, if we have other values for x, such as x = -1, x = 0, x = 1, and x = 2, we can follow the same steps as before for each value of x. Then, we need to evaluate the function for each value of x as follows:
x = -1

x = 0
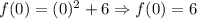
x = 1
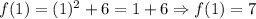
x = 2
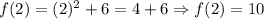
Now, to graph the function, we have the other ordered pairs as follows: (-1, 7), (0, 6), (1, 7), (2, 10).
Then, we can graph those points as follows:
As we can see, this is the graph of a parabola, with vertex (0, 6).
We can see more clearly if we use a graphing calculator as follows:
In summary, to graph the function, we need to evaluate the function for each value of x following the "rule" of the function, in this case we have: