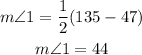Given that HC is the diameter of the circle, then:
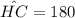
From the diagram, HC can be expressed as follows:
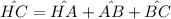
Substituting with HC = 180°, HA = 83°, and BC = 50°, and solving for AB:
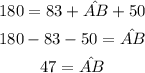
The relation between the angle outside the circle, ∠1, and the intersected arcs AB and HD are:
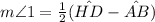
Substituting with HD = 135°, and AB = 47°, we get: