Question

HELP ASAP!! A direct variation function contains the points (-9, -3) and (-12, -4). Which equation represents the function?1. y = -3x2. y = -x/33. y = x/34. y = 3x

Answer 1

y = x/3 (option 3)

Step-by-step explanation:

To determine the equation that represents the function, first we will find the slope.

points (-9, -3) and (-12, -4)

`\begin{gathered} \text{slope = }m\text{ = }(y_2-y_1)/(x_2-x_1) \\ \end{gathered}`
`\begin{gathered} m\text{ = }\frac{-4_{}-(-3)_{}}{-12_{}-(-9_{})}\text{ = }(-4+3)/(-12+9) \\ m\text{ =}(-1)/(-3)\text{ = 1/3} \end{gathered}`

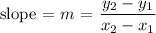
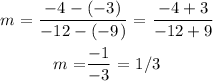
Then we will insert the value of the slope in the equation of a straight line:

y = mx + c

y = 1/3 (x) +c

where c = 0

y = x/3 (option 3)