Question

How do I find the angles of a obtuse triangle by using the side lengths and hypotenuse

Answer 1

We can calculate the angles of the triangle using the Law of Sines and Cosines.

The following parameters are provided for the triangle:

`\begin{gathered} a=45 \\ b=32 \\ c=24 \end{gathered}`

Measure of ∠A

The law of cosines can be applied as follows:

`\begin{gathered} a^2=b^2+c^2-2bc\cos A \\ \therefore \\ A=\arccos((b^2+c^2-a^2)/(2bc)) \end{gathered}`

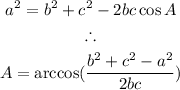
Substituting known values, we have:

`\begin{gathered} A=\arccos((32^2+24^2-45^2)/(2*32*24)) \\ A=106.1\degree \end{gathered}`

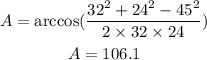
Measure of ∠B

We can apply the law of sines as follows:

`\begin{gathered} (a)/(\sin A)=(b)/(\sin B) \\ \therefore \\ B=\arcsin((b\sin A)/(a)) \end{gathered}`

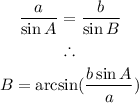
Substituting known values, we have:

`\begin{gathered} B=\arcsin((32*\sin106.1)/(45)) \\ B=43.1\degree \end{gathered}`

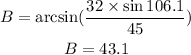
Measure of ∠C

The sum of angles in a triangle is 180 degrees. Therefore, the measure of angle C is:

`\begin{gathered} C=180-A-B \\ C=180-106.1-43.1 \\ C=30.8\degree \end{gathered}`

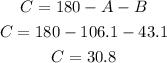
ANSWERS