Question

Finn has a piggy bank with 7 pennies, 1 dime, and 2 nickels. He will randomly choose 2 coins from the piggy bank one at a time without replacement. What is the probability that Finn will choose a penny first and then a dime?

Answer 1

First, let's calculate the total amount of coins:

`7+2+1=10`

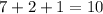
Since there are 7 pennies among the 10 coins, the probability of picking a penny is:

`P_1=(7)/(10)`

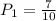
Then, there will be 9 coins, from which only 1 is a dime, so the probability of the second pick being a dime is:

`P_2=(1)/(9)`

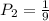
Now, to calculate the final probability, let's multiply both probabilities above:

`\begin{gathered} P=P_1\cdot P_2 \\ P=(7)/(10)\cdot(1)/(9) \\ P=(7)/(90) \end{gathered}`

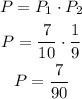
Therefore the probability is 7/90.