Question

Find the sum of the first 16 terms in an arithmetic series where a1 = 2, and the common difference is d=2.

Answer 1

The formula to find the sum of the first n-terms in an arithmetic series is:

`S_n=(n(a_1+a_n))/(2)`

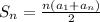
Where n is the number of terms, a1 is the first term and an is the last term.

Now, we know a1=2 and the common difference is d=2, with this information we can find a16 by using the following formula:

`a_n=a_1+(n-1)d`

Then, replace n=16, a1=2 and d=2 and solve:

`\begin{gathered} a_(16)=2+(16-1)\cdot2 \\ a_(16)=2+15\cdot2 \\ a_(16)=2+30 \\ a_(16)=32 \end{gathered}`

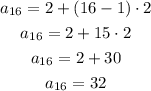
Now replace this value into the formula of the sum and solve:

`\begin{gathered} S_(16)=(16\cdot(2+32))/(2) \\ S_(16)=(16\cdot(34))/(2) \\ S_(16)=(544)/(2) \\ S_(16)=272 \end{gathered}`

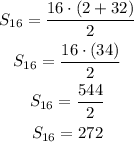
The answer is D. 272