Question

Find an equation of the hyperbola having foci at(1, -5) and (11,-5) and vertices at (2, -5) and (10, -5).

Answer 1

In this problem, we have an equation of the form

`((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1`

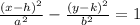
where

(h,k) is the center of the hyperbola

step 1

Find out the center

The center is the midpoint between the foci or between the vertices

the x-coordinate of the center is

x=(2+10)/2=6

the y-coordinate of the center is -5 (the same y-coordinate of the foci)

(h,k)=(6,-5)

step 2

Find out the value of a

Remember that

The coordinates of the vertices are

(h+a,k) and (h-a,k) ----------> (2,-5) and (10,-5)

so

h+a=2 -----> 6+a=2 --------> -4