Question

What is the de Broglie wavelength of a bullet of mass 0.075 kg traveling at 350 m/s? Planck's Constant is 6.63 × 10−34 J⋅s.4.1 × 10−^35 m2.5 × 10−^35 m2.2 × 10−^34 m1.7 × 10−^34 m

Answer 1

We are asked to determine DeBroglie's wavelength of a bullet. Let's remember that DeBroglie's wavelength is the ratio of Plank's constant and the momentum of the particle, therefore, we have the following formula:

`\lambda=(h)/(p)`

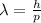
Where:

`\begin{gathered} \lambda=\text{ wavelength }\lbrack m\rbrack \\ h=\text{ Plank's constant }\lbrack Js\rbrack \\ p=\text{ momentum }\lbrack kg(m)/(s)\rbrack \end{gathered}`

The momentum of the particle is the product of the mass and the velocity, therefore, we have:

`p=mv`

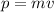
Substituting in the formula for the wavelength:

`\lambda=(h)/(mv)`

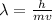
Now, we substitute the values:

Now we solve the operations:

`\lambda=2.5*10^(-35)m`

Therefore, DeBroglie's wavelength is 2.5 x 10 ^-35 meters.