Given:
The mas of the skier is m = 54 kg
The height of the slope is h = 67 m
The skier starts from rest.
Required: The speed of the skier on reaching the bottom of the slope.
Step-by-step explanation:
As the skier was initially at rest.
The initial speed will be zero.
According to the conservation of energy, mechanical energy is constant( it is the sum of kinetic energy and potential energy)
The kinetic energy is given by the formula
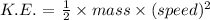
The potential energy is given by the formula
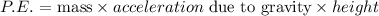
The acceleration due to gravity is denoted by g and its value is equal to 9.8 m/s^2.
At the top of the slope, the speed is zero so the kinetic energy is zero.
Here, the entire energy is due to potential energy.
The total energy is equal to
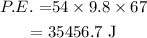
At the bottom of the slope, the potential energy is zero as the height is zero.
Here, the entire energy is due to kinetic energy.
The value of kinetic energy at the bottom of the slope is equal to the potential energy at the top of the slope.
The speed at the bottom of the slope can be calculated as
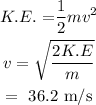
Final Answer: The speed of the skier at the bottom of the slope is 36.2 m/s