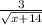Question

Find dy/dx of 6 times the square root of x +14

Answer 1

Given the equation:

`y=6√(x+14)\text{ ----- equation 1}`

Equation 1 can be expressed in a simpler manner to be

`y=6(x+14)^{\frac{1}{2\text{ }}}----\text{ equation 2}`

To find

`(dy)/(dx)`

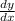
we take the derivative of y with respect to x.

From the product rule,

`(d(UV))/(dx)=U(dV)/(dx)+V(dU)/(dx)`

In this case,

`\begin{gathered} U=6 \\ V=(x+14)^{(1)/(2)} \end{gathered}`

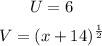
thus,

`\frac{d(6(x+14)^{(1)/(2)})}{dx}=6\frac{d((x+14)^{(1)/(2)})}{dx}+(x+14)^{(1)/(2)}(d(6))/(dx)`
`\begin{gathered} \frac{d((x+14)^{(1)/(2)})}{dx}=(1)/(2)(x+14)^{-(1)/(2)}*1 \\ =(1)/(2)(x+14)^{-(1)/(2)} \\ (d(6))/(dx)=0 \\ The\text{ derivative of a constant gives zero} \end{gathered}`

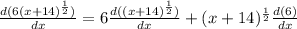
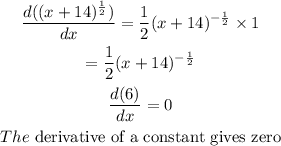
Substituting these parameters into the product rule equation, we have

`\begin{gathered} \frac{d(6(x+14)^{(1)/(2)})}{dx}=6((1)/(2)(x+14)^{-(1)/(2)})+(x+14)^{(1)/(2)}(0) \\ =3(x+14)^{-(1)/(2)}+0 \\ thus, \\ (d(6√(x+14)))/(dx)=(3)/(√(x+14)) \end{gathered}`

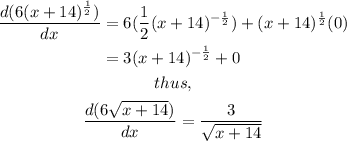
Hence, the derivative is expressed as

`(3)/(√(x+14))`