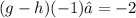Question

suppose that the functions g and h are defined for all real numbers x as follows. g(x)=x+1 h(x)=2x^2. write the expressions for (g+h)(x) and (g*h)(x) and evaluate (g-h)(-1)

Answer 1

EXPLANATION

Given the functions:

g(x) = x+1 and h(x) = 2x^2

First, the expression (g+h)(x) will be as shown as follows:

Assign the function g=x+1

=( x + 1 + h(x) ) (x)

Assign the function h=2x^2

`\mleft(g+h\mright)\mleft(x\mright)=2x^2+x+1`

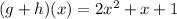
(g*h)(x):

Assign the function g=x+1

=((x+1)h(x))(x)

Assign the function h= 2x^2

=(x+1)*2x^2

Expanding (x+1)*2x^2

=2x^3+2x^2

`\mleft(g\cdot h\mright)\mleft(x\mright)=2x^3+2x^2`

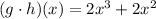
(g-h)(-1)​:

Assign the function g=x+1

=(x+1 -h(x)) (x)

Assign the function h=2x^2

=(x+1-2x^2)(-1)

Evaluating (x+1-2x^2)(-1): -2

=-2

`\mleft(g-h\mright)\mleft(-1\mright)​=-2`